In this rather popular video, Vi Hart experiments with the patterns that can be formed by connecting the vertices of a regular polygon with straight lines of equal length.

In addition to the obvious number-theoretic interpretation, there is a nice group-theoretic interpretation that generalises well to higher dimensions. For instance, Vi Hart’s ‘square star’ composed of four squares can be thought of as a 3-tuple, namely:

• The full group G = D32 of symmetries of the star;
• A normal subgroup H = D8 of symmetries fixing each of the components;
• The quotient group G/H = C4 of cyclic permutations.

With two dimensions, these things are really easy to find, and completely classified by Vi Hart’s video. On the other hand, the multidimensional analogues are really exceptional objects. The standard five-pointed pentagram has four three-dimensional versions, the Kepler-Poinsot polyhedra, and ten four-dimensional analogues, the Schläfli-Hess polychora. One of the Kepler-Poinsot polyhedra is the small stellated dodecahedron, immortalised in card by Joseph Myers:

Of course, for the group theory to come into play non-trivially, we are interested in examples where we have a compound of polytopes, analogous to the six-pointed Star of David. Together with the restriction that both the convex hull and constituent polytopes are regular, the only possibilities are:

• Three 16-cells in four dimensions, with the same vertices as a 24-cell (quotient S3).
• Two tetrahedra in three dimensions, with the same vertices as a cube (quotient C2).

If the convex hull is not required to be regular, then other possibilities include two dual 24-cells in four dimensions, two dual simplices (in any number of dimensions), and six 16-cells in four dimensions (by combining two of the previous results).

Anyway, the unique three-dimensional example is the stella octangula, a compound of two dual tetrahedra. It appears twice in Escher’s Stars, and there’s even a variant of the Rubik’s cube based on it. As one can imagine, it has also been constructed by Joseph Myers:

The visible surface can also be obtained by gluing eight regular tetrahedra to an octahedron, in the way that occurs in the dual tiling to the rhombic dodecahedral honeycomb.

Stella octangula numbers

By analogy with triangular numbers, square numbers and tetrahedral numbers, the sequence of stella octangula numbers has been investigated. For instance, 245 is a stella octangula number, since we can fill a stella octangula with 245 spheres in a FCC arrangement:

David Eppstein has even assembled 124 magnetic balls into a stella octangula, for the Wikipedia article on stella octangula numbers.

As with all three-dimensional figurate numbers, they are values of a cubic polynomial. Hence, if we try to find stella octangula numbers which are also square, we have the standard problem of locating integer points on an elliptic curve, of which there are finitely many. It was proved that the only such numbers are 1 (trivially) and 9653449.

A similar problem is to find pyramidal numbers which are square. The single non-trivial solution to this is much more well-known: 1² + 2² + … + 24² = 70². This is intimately related to a particular construction of the Leech lattice, where one begins with a much simpler (25+1)-dimensional even unimodular lattice in Minkowski space, and chooses the 24-dimensional plane of null vectors orthogonal to the null vector (70; 1, 2, 3, …, 24).

Usually, it is very difficult to find a reasonably naturally-defined sequence which is not present on the Online Encyclopedia of Integer Sequences. The OEIS contains everything from the ubiquitous Bernoulli numbers and the fascinating Golomb self-referential sequence, to such utterly pointless trivialities as A171056 (the primes, but where every ’7′ is replaced with a ’9′ and vice-versa in the decimal expansions). More examples on the entire spectrum were competitively evaluated over at the Aperiodical.

Hence, I was rather surprised to see that the following sequence does not feature:

2, 6, 14, 22, 30, 34, 38, 42, 58, 66, 70, 78, 86, 94, ...

The motivation for this sequence was the observation that the numbers {2013, 2014, 2015} are each squarefree and have three prime factors. Ignoring the second condition, we can consider runs of consecutive squarefree numbers. Clearly, the longest such runs have length 3 (as in this example), since no multiple of 4 can possibly be squarefree.

• Definition: A positive integer N is described as comfortably squarefree if N − 1, N and N + 1 are all squarefree.

It is not difficult to obtain an infinite product expansion for the asymptotic density of comfortably squarefree numbers. An integer N is comfortably squarefree if and only if for every prime p, the residue of N modulo p² is not in the set {−1, 0, 1}. With a slight amount of work, this leads to the following asymptotic density:

If that 3 is replaced with a 1, it yields the density of squarefree integers, . Unfortunately, this does not appear to have a closed form. Numerically, I have evaluated δ ≈ 0.125486980906, where the final digit may be slightly off. Plugging this into Robert Munafo’s RIES doesn’t return anything, which is a shame as it is usually good at finding these sorts of things.

Even more bizarre is the fact that pairs of consecutive squarefree numbers have been investigated, mentioned at the end of the MathWorld article, and heavily featured on the OEIS. Hence, not believing that triples of consecutive squarefree numbers could possibly be a new concept, I searched this on Google (yes, this came after deriving the asymptotic density and numerically computing it!) and sure enough there was a MathOverflow question asking whether there are infinitely many examples.

Anyway, I’ll upload the sequence of comfortably squarefree numbers to the OEIS tomorrow, assuming no-one beats me to it.

A fascinating paper by Louis Kauffman establishes the equivalence of the four-colour theorem (the assertion that any planar graph can have its vertices coloured with one of four colours, such that neighbouring vertices have different colours) to the following seemingly unrelated combinatorial statement:

• Let n be a positive integer, and let A and B be two complete parenthesisations of the expression , where × is the three-dimensional cross product. Then we can assign each of to be either i, j or k such that the two expressions are non-zero and equal.

Moreover, the proof is not particularly complicated. Firstly, we shall examine other restatements of the four-colour theorem.

Vertex, face and edge colourings

In its simplest form, the four-colour theorem states that we can colour the vertices of a planar graph with at most four colours, such that no adjacent vertices have the same colour. For example, take the graph of the icosahedron, which is indeed planar:

Tait proved that this is equivalent to the statement that every bridgeless planar 3-regular graph can have its edges coloured with three colours, such that every vertex is incident with precisely one edge of each colour. It’s not too difficult to reconstruct the intermediate steps without ever having seen the proof, just by knowing the two propositions and by employing reasoning.

Firstly, note that Tait’s statement is about planar graphs where every vertex has degree 3. Conversely, the worst-case scenario of the original statement is where every face is a triangle (since any planar graph can be ‘triangulated’ into this form). Hence, a good idea is to form the planar dual of the worst-case scenario of the original statement:

We can colour the faces of a 3-regular plane (or spherical) graph with four colours, such that no two faces of the same colour share a common edge.

The 4-colouring of the vertices of the icosahedral graph, for instance, is equivalent to the following 4-colouring of the faces of the dodecahedral graph:

Now, to convert this to a 3-colouring of the edges, we want to somehow assign a colour to an edge based on the colours of the neighbouring regions, and to do this in a nicely reversible way. To do so, let the regions be coloured with elements of the Klein 4-group, and the edges be coloured by the product of the two regions. Since it’s Abelian and every element is its own inverse, we obtain a colouring of the edges with the non-identity elements of the Klein 4-group. Supposing that yellow is the identity, we get the following edge-colouring:

This establishes the equivalence of the four-colour theorem and Tait’s restatement. Not too difficult, was it? Now, we can start to see the similarity with Kauffman’s combinatorial problem. If we ignore the signs of the vectors, then the colours of these edges can be the three unit vectors i, j, k, and the vertices correspond to the cross product operation. Parenthesisations are equivalent to binary trees, so (temporarily ignoring signs) Kauffman’s combinatorial problem is just Tait’s restatement applied to the special case of graphs obtained from gluing two equally-sized trees together.

Dealing with signs

One of the subtleties is that it is not immediately obvious that we would necessarily get A = B, rather than A = −B. To overcome this, Kauffman employed an idea by Roger Penrose of assigning either i or −i (complex numbers, not quaternions or unit vectors!) to each vertex, depending on whether the colours of the three edges are arranged in clockwise or anticlockwise order. Then, Kauffman shows that the product of the vertices is 1, which is equivalent to the signs working out correctly.

Proofs of the four-colour theorem

The first correct proof of the four-colour theorem was Appel and Haken’s massive case-bash, which relied on machine-checking each of 1936 configurations for reducibility. Essentially, they proved that any counter-example to the four colour theorem could be reduced to a smaller counter-example, so by induction the theorem is true.

Recently, a proof was announced of the snark conjecture, that any snark (bridgeless 3-regular graph with no 3-edge-colouring) must contain the Petersen graph as a minor. This is clearly a generalisation of Tait’s restatement of the four-colour theorem, which is the contrapositive of ‘no snark is planar’. The Petersen graph is both the simplest snark and the first to be discovered.

The Petersen graph is also a forbidden minor for the set of linklessly embeddable graphs (those which cannot be drawn in three-dimensional space without two cycles forming a Hopf link), so it follows that any bridgeless linklessly embeddable 3-regular graph must have a 3-edge-colouring, generalising Tait’s restatement of the four-colour theorem.

The proof of the snark theorem is largely unpublished, although apparently it is another computer-assisted proof. Hence, it (unfortunately!) does not provide a counter-example to Doron Zeilberger’s ultimate fantasy of the four-colour theorem having no ‘human’ proofs.

Breaking news: Patrick Stevens (whom you may recognise from the cp4space cipher-solving leaderboard) has published a collection of poems pertaining to Sylow’s theorems.

Anyway, on the real projective plane, there are a couple of geometric theorems worth mentioning. The thing that’s interesting about Pappus’ theorem and Desargues’ theorem is not that they apply to the real projective plane, but rather that whether or not these theorems apply to a particular projective plane can be used to deduce properties of how the plane was constructed. I’ll start by stating the theorems:

Pappus’ theorem: If we have eight of the nine concurrences shown in the diagram above, then the ninth also holds. In the complex projective plane, this follows from the Cayley-Bacharach theorem.

Desargues’ theorem: Two triangles are in perspective about a point if and only if they are in perspective about a line (see above). Equivalently, suppose we have a collection of 10 points and 10 lines, associating an ordered pair (p(V), l(V)) of a point and a line to each vertex V of the Petersen graph, where each edge is replaced with a zweibeck (pair of oppositely directed edges). We consider each directed edge X → Y to represent the point p(X) and the line l(Y). Desargues’ theorem states that if 29 of these correspond to incidences (a point lying on a line), then so does the thirtieth.

A German mathematician called Hessenberg proved that Desargues’ theorem can actually be deduced from Pappus’ theorem. In other words, all Pappian projective planes are also Desarguesian. For example, the real and complex projective planes, and the projective planes of finite order, are all Pappian, so thus Desarguesian.

The converse of Hessenberg’s theorem is not true, however. The quaternionic projective plane is Desarguesian, but not Pappian. It transpires that this is a consequence of the quaternions being non-commutative. Indeed, the following have been proved:

• Every Desarguesian plane can be constructed from a skew-field F, by working in the vector space F³, discarding the origin and identifying scalar multiples of a point. The converse is also true.
• The Pappian planes are precisely those constructed from a commutative field F.

This is quite remarkable, since non-Desarguesian planes can be really bizarre. Some correspond to this sort of construction (e.g. the octonionic projective plane, or Cayley plane), whereas others are downright pathological (e.g. the Moulton plane).

If a plane can be embedded in a three-dimensional projective space, it is automatically Desarguesian. Consequently, it is impossible tohave an octonionic 3-space , as that would imply that the Cayley plane is Desarguesian (which it isn’t). The proof of this is quite simple, and follows from letting ABC and A’B'C’ in the diagram be triangles in different planes (so A”B”C” must trivially be the line where the planes intersect), and projecting down into two dimensions.

For this cipher, I have encoded the information in a list of real numbers. Ordinarily, these would be complex, but I managed to circumvent this. Unfortunately, the ciphertext is thus longer than it needs to be. Really, it’s twice as large as necessary. In any case, there is a solvers’ area accessible by a password in the plaintext. Either solve the cipher (as most people do), or guess it; it’s your choice. Rendered below is the aforementioned cipher:

756.5, -26.7, -33.3, -40.6, -4.7, -64.5, 12.0, 30.3,
-15.3, -29.6, -21.4, -12.2, -23.4, -16.6, -48.4, -13.1,
32.8, -24.5, 32.5, -6.3, 11.5, 65.1, -16.9, -1.9,
6.3, -24.3, 17.3, -38.3, -23.5, 32.1, 26.2, 31.2,
-12.0, 31.2, 26.2, 32.1, -23.5, -38.3, 17.3, -24.3,
6.3, -1.9, -16.9, 65.1, 11.5, -6.3, 32.5, -24.5,
32.8, -13.1, -48.4, -16.6, -23.4, -12.2, -21.4, -29.6,
-15.3, 30.3, 12.0, -64.5, -4.7, -40.6, -33.3, -26.7

Given a real number x, computing its continued fraction can reveal a lot of information. In the simplest case, the continued fraction terminates if and only if the number is rational. One particular example of this is the rational , the continued fraction of which is shown below:

(The square-bracketed expression [3; 7, 16] is just a convenient notation for the continued fraction expansion.)

Rational numbers are simply the roots of linear polynomials with integer coefficients. Hence, the next simplest case is when x is the root of a quadratic equation with integer coefficients. It transpires that this is equivalent to the continued fraction being eventually periodic, such as , where the sequence (2, 1, 3, 1, 2, 8) is repeated indefinitely.

Roots of higher-degree irreducible polynomials, along with transcendental numbers, all have aperiodic continued fractions. Some of these are simple and predictable, such as , whereas others seem to exhibit no obvious patterns, such as π. However, this article is concerned with algebraic numbers rather than transcendental ones, so the next cases to explore are roots of cubics.

Brillhart’s cubic

In 1965, Brillhart noticed that the positive real root of the depressed cubic x³ − 8x − 10 has an ‘exotic’ continued fraction. This algebraic number is equivalently the dominant eigenvalue of the following 3 × 3 matrix:

What makes the continued fraction exotic is the presence of large terms early in the expansion:

[3; 3, 7, 4, 2, 30, 1, 8, 3, 1, 1, 1, 9, 2, 2, 1, 3, 22986, 2, 1, 32, 8, 2, 1, 8, 55, 1, 5, 2, 28, 1, 5, 1, 1501790, 1, 2, 1, 7, 6, 1, 1, 5, 2, 1, 6, 2, 2, 1, 2, 1, 1, 3, 1, 3, 1, 2, 4, 3, 1, 35657, 1, 17, 2, 15, 1, 1, 2, 1, 1, 5, 3, 2, 1, 1, 7, 2, 1, 7, 1, 3, 25, 49405, 1, 1, 3, 1, 1, 4, 1, 2, 15, 1, 2, 83, 1, 162, 2, 1, 1, 1, 2, 2, 1, 53460, 1, 6, 4, 3, 4, 13, 5, 15, 6, 1, 4, 1, 4, 1, 1, 2, 1, 16467250, 1, 3, 1, 7, 2, 6, 1, 95, 20, 1, 2, 1, 6, 1, 1, 8, 1, 48120, 1, 2, 17, 2, 1, 2, 1, 4, 2, 3, 1, 2, 23, 3, 2, 1, 1, 1, 2, 1, 27, 325927, 1, 60, 1, 87, 1, 2, 1, 5, 1, 1, 1, 2, 2, 2, 2, 2, 17, 4, 9, 9, 1, 7, 11, 1, 2, 9, 1, 14, 4, 6, 1, 22, 11, 1, 1, 1, 1, 4, 1, 3, 2, 1, 2, 1, 1, 2, 4, 2, 1, 5, 1, 8, 2, 2, 5, 1, 2, 1, 1, 1, 1, 1, 3, ...]

To understand why that occurs, it helps to have an exact closed form for the root. Fortunately, that’s not too hard, since we know how to solve a depressed cubic. In particular, we equate x³ − 8x − 10 with the ‘difference of three cubes’ x³ + a³ + b³ − 3abx. Equating coefficients, we get:

• a³ + b³ = −10
• ab = 8/3

We can easily solve the resulting quadratic equation to obtain a and b. Then, the real root is simply x = −(a + b), which is given by:

Note that the is significant, as 163 is a Heegner number (the ring of integers in the quadratic field is a unique factorisation domain). The reason for the large partial quotients in the continued fraction expansion was explained by Stark, who incidentally was the first person to correctly prove Gauss’s conjecture that the Heegner numbers are precisely {1, 2, 3, 7, 11, 19, 43, 67, 163}.

Some mathematical objects are completely boring. Others have a few interesting properties. The Petersen graph, by comparison, has a plethora of quite remarkable features that, taken alone, would each qualify the graph as being interesting. I’ve mentioned this graph a few times before, but this is the first post exclusively dedicated to it. Firstly, here’s a picture of the graph:

For completeness, I’ll mention that it’s a 3-regular graph with 10 vertices and 15 edges, and that it is both vertex- and edge-transitive. Now, let’s discuss why it’s interesting:

1. Linklessly embeddable graphs

Wagner’s theorem is well known, and states that a graph is non-planar if and only if it contains either the complete graph K5 or the bipartite graph K3,3 as a graph minor. The Petersen graph has both of these as minors, so it is really non-planar! It has the stricter property that if you draw the Petersen graph in three-dimensional space (with no edges crossing), you can necessarily find two linked cycles.

In fact, like planar graphs, the linklessly embeddable graphs are closed under the operation of taking graph minors. The Petersen graph, together with K6 and five other graphs, form a finite set of forbidden minors (the existence of which is guaranteed by the Robertson-Seymour theorem together with Zorn’s lemma). They all have 15 edges, and can be interconverted by delta-wye transformations.

2. Toroidal and projective-plane embeddings

In the previous section, I mentioned how the Petersen graph is linklessly embeddable, therefore far from being planar. Consequently, removing any vertex of the Petersen graph leaves a non-planar graph. Hence, it is somewhat surprising that it can be drawn on the surface of a torus without any edges crossing. Indeed, it can be shown that every generalised Petersen graph (formed by taking the skeleton of a regular n-gonal prism and replacing one of the terminal n-gons with a regular star n-gon) is toroidal.

The Petersen graph has a more natural and very symmetric embedding on the projective plane. It can be obtained by drawing a regular dodecahedron on the surface of a sphere, and identifying antipodal points, edges and faces. This results in an abstract polyhedron called the hemi-dodecahedron, the skeleton of which is the Petersen graph. The hemi-dodecahedron and hemi-icosahedron can then be used to construct even more pathological polytopes, the 11-cell and the 57-cell.

3. Construction as a Kneser graph

The hemi-dodecahedron has 60 symmetries, abstractly isomorphic to the alternating group A5. It follows that the automorphism group of the Petersen graph must contain A5 as a subgroup. You may intuitively think that it is precisely A5, but the subtle operation of ignoring the faces of the hemi-dodecahedron could result in additional automorphisms.

It transpires that this is indeed the case, and the Petersen graph has 120 symmetries, abstractly isomorphic to S5. The easiest way to see this is to construct the Petersen graph as a Kneser graph. Specifically, each vertex is associated with a subset of {a,b,c,d,e} of cardinality 2, and two vertices are joined with an edge if the corresponding subsets are disjoint.

To show that the only symmetries are the permutations of {a,b,c,d,e}, it suffices to demonstrate that we can recover the elements from the graph. We describe a pair of edges x, y as maximally distant if no vertex of x is connected to any vertex of y. It can easily be seen that if we select an edge x, we can find precisely two edges y, z maximally distant from x. Also, y and z are maximally distant from each other.

Hence, the 15 edges of the Petersen graph uniquely and naturally partition into 5 subsets of three edges. These are bijected with the elements of {a,b,c,d,e}, where the six vertices belonging to the union of the three edges are those not containing that element. This completes the proof that the symmetries of the Petersen graph are exactly the permutations in S5.

4. Not a Cayley graph

I’ve mentioned that it is vertex-transitive, that is to say that there are symmetries taking any one vertex to any other (or, equivalently, that every vertex is ‘essentially the same’). Graphs with this property are ten-a-penny, such as the following:

These are Cayley graphs of the groups C4, C7 and D10, respectively (N.B. a group can have multiple Cayley graphs, depending on which generators are used). Every Cayley graph is vertex-transitive (by construction), but not all vertex-transitive graphs are Cayley. The smallest counter-example is, unsurprisingly, the Petersen graph.

5. Hypohamiltonian

A graph is described as Hamiltonian if we can find a cyclic tour, which visits every vertex exactly once. Most vertex-transitive connected graphs are Hamiltonian, and it is conjectured that there are only five counter-examples. The smallest of these is really trivial, being the complete graph K2 (once the edge is traversed, you cannot return). The others are the Petersen graph, the Coxeter graph, and two larger graphs derived from the Petersen and Coxeter graphs.

However, removing any vertex leaves a Hamiltonian graph, so the Petersen graph is described as hypohamiltonian. We can see that this is the case by using vertex-transitivity (hence only one vertex needs to be considered) and observing the following drawing of the Petersen graph:

Indeed, the Petersen graph is the smallest hypohamiltonian graph.

6. Snarks

In an earlier post, I mentioned how the four-colour theorem is equivalent to showing that no snark is planar. A snark, by the way, is a 3-regular connected graph with no isthmus* (edge whose removal would result in a disconnected graph), such that we cannot 3-colour the edges such that each vertex is incident with one edge of each colour. The dodecahedral graph, for example, is 3-regular, connected and bridgeless**, but not a snark as it admits the following edge tricolouring:

The Trinity mathematician William Tutte, whom you may know from such things as the cryptanalysis of the Lorenz cipher in the Second World War and the discovery of the first perfect squared square, conjectured that every snark has the Petersen graph (the smallest snark) as a graph minor. This was proved recently, with the four-colour theorem following as a corollary.

* Some people use the alternative term ‘bridge‘. I am not one of those people…

** …but nevertheless, I do admit that ‘isthmusless’ sounds clumsy.

7. Desargues’ theorem and right-angled hexagon theorem

Even more recently, I wrote about Pappus’ theorem and Desargues’ theorem. The latter can be interpreted as a statement about the Desargues graph (bipartite double cover of the Petersen graph), or equivalently about the Petersen graph itself. Another theorem involving the Petersen graph is this one, mentioned in an e-mail from John Conway:

Suppose we have 10 lines in Euclidean 3-space, corresponding to the vertices of the Petersen graph. To each edge, we assign the statement ‘the lines corresponding to the two endpoints intersect at right angles’. If fourteen of the statements are true, then so is the fifteenth (thereby constituting a rather impressive example of (15,14)-TFAE).

Anyway, I suppose I ought to explain what a bipartite double cover is. Basically, we replace each vertex of the Petersen graph with a red vertex and a blue vertex, joining two vertices in the resulting graph if the vertices are different colours and the parent vertices were connected by an edge. What results is the 30-edge 20-vertex Desargues graph:

This is a different from the dodecahedral graph, which can also be regarded as a double cover of the Petersen graph.

8. The Hoffman-Singleton theorem

The Petersen graph has diameter 2 and girth 5. In other words, the shortest cycle has length 5, and any two vertices are either adjacent or share a common vertex. This is equivalent to a set of constraints posed in an AMS question. Ignoring the empty graph, the only possible graphs are:

• The 5-vertex 2-regular pentagon;
• The 10-vertex 3-regular Petersen graph;
• The 50-vertex 7-regular Hoffman-Singleton graph;
• A particular 3250-vertex 57-regular graph whose existence and uniqueness are unknown.

Intriguingly, the Hoffman-Singleton theorem has reduced the problem of finding all graphs with this property to a finite case-bash, but where ‘finite’ is still prohibitively large for an exhaustive search. This is a counter-example to the common misconception that all finite problems are trivial.

9. Induced subgraphs

The Petersen graph appears as an induced subgraph in many larger interesting graphs. The aforementioned Hoffman-Singleton graph is one such example, as is the Clebsch graph (a 16-vertex 5-regular graph, such that the removal of any vertex and its five neighbours leaves the Petersen graph).

The Clebsch graph can be constructed by taking a tesseract and joining pairs of opposite vertices. It is interesting in that the edges of K16 can be partitioned into three copies of the Clebsch graph, resulting in a 3-colouring of K16 with no monochromatic triangle. This, combined with a trivial upper bound, establishes the Ramsey number R(3,3,3) = 17.

Naturally, the Petersen graph appears infinitely often as an induced subgraph of the Rado graph, as noted by Gabriel Gendler in his cp4space guest post.

10. Cycle-continuous maps

A map from (the edges of) a graph G to a graph H is described as cycle-continuous if the pre-image of any Eulerian subgraph is also Eulerian. This definition is similar to that of continuity in a general topological space, but with Eulerian subgraphs instead of open sets. Jaeger conjectured that any bridgeless graph can be mapped cycle-continuously into the Petersen graph, and demonstrated that (if true) this would imply three more open conjectures for free:

• The cycle double cover conjecture (conjectured by Szekeres);
• Every bridgeless graph has a nowhere-zero 5-flow (conjectured by Tutte);
• The Berge-Fulkerson conjecture.

Conclusion

In summary, there are at least as many interesting properties of the Petersen graph as there are vertices. I shall end on a quotation in true oratory style, mentioning that Donald Knuth (inventor of LaTeX, used by mathematicians and prophylactic manufacturers alike!) described the Petersen graph as:

“a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general”

This is classically used as a rudimentary compression algorithm, although it also makes for a nice cipher challenge.

000011010110111 0100001111000111 1110 11000011100111101101001
001011101010100111 110100101
01001110100111110001010110001110111101111011010,
001001110101101001101010 11100111 1110
01100100000101001010011111101010 0000101100100,
0011001101011010010110 01011001100010101100011110010100000111
1111010000000010001010111 0011010110000110
01001110111111110110100111 110100101
001000111001011011111011000011110100 1111010010101100110000110
111111001100011001010111111001010000 11011010 0000110100
01011001111011100001011001000100
00101010110000100100101000100101001001110010. 0000110100
110001111001110111001101101010111111 10110111
1111110010101111101011011000101101001.

Good luck.

(This post is completely unrelated to the category of cones. Apologies if you were mistakenly directed here by a fuzzy search engine.)

In May 2013, the category theorist Dr Eugenia Cheng (whom you may recognise from her quotations on the Imre Leader Appreciation Society) wrote a paper on the ideal cream tea. This received a lot of media attention, including from the Daily Mail, Telegraph and The Aperiodical (in increasing order of accuracy).

The paper discusses the optimal proportions of cream, strawberry preserve and scone for an ideal cream tea. Unlike most academic papers, this one has an accompanying video:

I was slightly disappointed that there was no category theory in the paper, despite the author being a category theorist. It did, however, explicitly mention that the preserve should be added before the cream, in the style of the Cornish. By comparison, residents of Devon advocate the reversed approach of adding the cream first. The fact that these are genuinely different outcomes can be neatly abstracted into the statement that this diagram in the category of scones does not commute:

The other shortcoming of Eugenia Cheng’s otherwise brilliant paper is that it doesn’t mention that cream teas can be augmented by the addition of a bisected strawberry, as in the image below. The left-hand scone has been prepared using the Devonian order of morphism composition, whereas the right-hand scone has been prepared using the (strictly superior) Cornish method:

Jacob Aron mentioned on Twitter that if the scone has a diameter of 2 centimetres, the clotted cream would need to be infinitely tall, distributed in the form of a Dirac delta function† , where V is the desired volume of cream.

† Disclaimer: This is not a function in the pure-mathematical sense.

Flexagons

There have been other recent examples of gastronomical mathematics in the last year. I presume that you’ve seen the integral banana I posted several months ago. Additionally, Evelyn Lamb has reviewed a multitude of videos involving both mathematics and food, including the culmination of Vi Hart’s flexagon series of videos.

Evident from the construction of the simplest hexaflexagon is that we are dealing with a Möbius strip, which is folded to form a multiple cover of the hexagon. The automorphisms of the Möbius strip (C18) quotiented by the automorphisms of the resulting hexagon (C6) gives the group of flexations (C3).

With three of the strips used to build a hexaflexagon, one can also construct a Boerdijk-Coxeter helix. Twenty cyclic Boerdijk-Coxeter helices of 30 tetrahedra each are obtained by partitioning the 600-cell (a four-dimensional regular polytope) according to a discrete Hopf fibration.

I’ve been intending to write about the Leech lattice for a while now. I wanted to ensure that I could actually do it justice, and in particular make it strictly more comprehensive than the Wikipedia and Mathworld articles. The authoritative source on this topic is the book Sphere Packings, Lattices and Groups (Conway and Sloane), which is a compilation of papers by several authors.

A lattice, in this context, is a set of vectors in Euclidean space that form an Abelian group under addition. Equivalently, it is a set of points (including the origin), such that for any two points A and B, there exists a translation mapping A to B and leaving the lattice invariant. For example, the midpoints of the cells of the regular square and hexagonal tilings form lattices in two dimensions, familiar as the Gaussian and Eisenstein integers:

By comparison, this construction applied to the equilateral triangular tiling does not yield a lattice, since there is no translation capable of mapping an up-pointing triangle to a down-pointing one. Nevertheless, the set of points can be expressed as the disjoint union of two hexagonal lattices.

The hexagonal lattice can be regarded as the best lattice in two dimensions, for the following reasons:

• It offers a denser packing of unit discs than any other arrangement;
• It gives a thinner covering of overlapping discs than any other lattice;
• In the packing, each disc touches six others, which is trivially maximal.

The next time a single lattice wins all three awards is in 24 dimensions, with the spectacular Leech lattice. (The E8 lattice in eight dimensions comes close, but is slightly beaten by a lattice called A8* in the covering department.) The rest of this post is primarily concerned with the Leech lattice, although the E8 lattice will undoubtedly be mentioned a few times.

Characterisation and properties

So, what exactly is the Leech lattice? It turns out that it’s the only even integral unimodular lattice with no roots in fewer than 32 dimensions. Each of these terms will take some explaining:

• A lattice, as mentioned at the beginning of this article, is a set of vectors in Euclidean space which is closed under addition.
• A lattice is integral if the dot product of any two vectors is an integer.
• An integral lattice is described as even if the squared norm of any vectors is an even integer. Otherwise, it is an odd integral lattice.
• A lattice is unimodular if the fundamental parallelotope has unit volume, or the determinant of the generating matrix is ±1. Equivalently, the lattice has a density of one point per unit volume. Even integral unimodular lattices only occur in dimensions divisible by 8, with the unique example in 8 dimensions being the E8 lattice.
• For an even unimodular lattice, a root is a vector of squared norm 2. The Leech lattice has none of these, so the shortest nonzero vectors have a squared norm of 4 (or, equivalently, a length of 2).

Because the shortest distance between two lattice points is equal to 2, that means that we can place a ball of unit radius centred on each lattice point. Each sphere touches precisely 196560 others, which is the maximum for 24 dimensions. (The kissing number problem has also been solved in 1, 2, 3, 4 and 8 dimensions, with values of 2, 6, 12, 24 and 240, respectively, attained by the integer lattice, hexagonal lattice, FCC lattice, D4 lattice and E8 lattice, respectively.)

If we enlarge the spheres to a radius of √2, they will overlap and cover all space. Establishing that the covering radius is equal to √2 is non-trivial, and involves analysing all 23 types of deep hole (points maximally distant from lattice points) encountered in the Leech lattice. Each type of deep hole corresponds to one of the 23 other even unimodular 24-dimensional lattices, known as Niemeier lattices.

Coordinate-based constructions

Whilst saying ‘the unique even unimodular lattice in 24 dimensions with no roots’ is sufficient to characterise the Leech lattice, it is appallingly non-constructive. It’s a very complicated lattice, and it’s quite non-trivial to construct the Leech lattice. By comparison, it’s very easy to construct the cubic lattice:

• Points in such that all coordinates are integers

and it’s not much harder to construct the D4 lattice:

• Points in such that all coordinates are integers and the sum of coordinates is even

or even the E8 lattice:

• Points in such that either all coordinates are integers or all coordinates are half-integers, and the sum of all coordinates is even.

Conversely, constructing the Leech lattice using coordinates is really complicated! Even though the following definition is elementary, it involves lots of intermediate steps and is quite complicated indeed:

• Points in such that the coordinates are all integers congruent to m modulo 2, the sum of all coordinates is congruent to 4m modulo 8, and such that for each i in {0, 1, …, 11}, the (i + 12)th coordinate is congruent modulo 4 to the sum of the jth coordinates over all j in {0, 1, …, 11} such that (i, j) does not describe an edge of the icosahedron with vertices labelled {0, 1, …, 11}. Then scale the resulting lattice by 1/√8 so that it is unimodular.

This elementary construction was obtained by taking the simplest construction based on the binary Golay code, together with a relatively simple construction of the binary Golay code itself, and combining them. It doesn’t seem to be a particularly motivated construction, though, and there are some simpler ones.

Laminated lattices

This is quite a fun way to create dense lattice sphere packings without much effort. We start with the ordinary integer lattice:

We now add an extra dimension (increasing it from 1 to 2), and place a sphere as low down as possible whilst resting on top of the lattice:

Now take the additive closure (i.e. make it closed under all translations mapping spheres to spheres):

Now imagine it horizontally embedded in three-dimensional space, and add an extra sphere as low down as possible whilst still resting on our hexagonal lattice of spheres. In the image below (plan view), I’ve added six of the spheres of the second layer, and two of the third layer:

Taking the additive closure gives the FCC lattice:

The sequence of laminated lattices obtained in this manner begins Z, A2 (hexagonal), A3 (FCC), D4, D5, E6, E7, E8, and gives rather dense lattices. The laminated lattices in 9 and 10 dimensions are also unique, but there are two types of deep hole in Λ10, giving two different choices for the laminated lattice Λ11. There are three laminated lattices in each of 12 and 13 dimensions, but remarkably instead of getting an exponential explosion of possibilities, all routes converge to a unique laminated lattice in 14 dimensions.

This continues as a nice steady sequence of unique lattices, culminating in Λ24 being the Leech lattice itself! Note that this construction is much simpler than the direct coordinate-based approach using the binary Golay code. However, when one wants to investigate the geometry of the Leech lattice, it is easier to work with the coordinate-based parametrisation.

This is followed by an explosion, as each of the 23 deep holes of the Leech lattice yield different laminated lattices in 25 dimensions, and not much is known about the plethora of laminated lattices in 26 dimensions or above. However, there is a very remarkable periodicity observed in one particular sequence of laminated lattices: the centre density (number of lattice points per unit volume) oscillates with period 24 (and is an even function), where the lattice is obtained by ‘gluing’ to the Leech lattice.

Eisenstein integers, Golay codes and Mathieu groups

We have thought of the Leech lattice in its most natural state, which is a 24-dimensional real lattice. Since the complex numbers can be identified with the real plane, this suggests a 12-dimensional complex representation of the Leech lattice. The construction using Gaussian integers is identical to the ordinary 24-dimensional real construction (since the Gaussian integers are isometric to the Cartesian product ), whereas the Eisenstein construction is distinct.

Instead of using the 24-dimensional binary Golay code over F2, it exploits the 12-dimensional ternary Golay code over F3. The ternary Golay code, whilst named after Golay, was actually discovered a couple of years earlier by a football pool enthusiast (see here). Incidentally, the binary and ternary Golay code constructions of the Leech lattice are two of 23 constructions, one for each Niemeier lattice. Conway and Sloane discuss these ‘holy constructions’ in Sphere Packings, Lattices and Groups.

It’s worth discussing the symmetry groups of these codes. The permutations of the coordinates that fix the binary Golay code form the Mathieu group M24, which has two other sporadic groups (non-Abelian simple groups not of Lie type), M23 and M22, as one- and two-point stabilisers. Similarly, the symmetries of the ternary Golay code give the sporadic group M12, which has M11 as a one-point stabiliser. M21 is isomorphic to PSL(3,4) therefore non-sporadic, and M10 isn’t even simple.

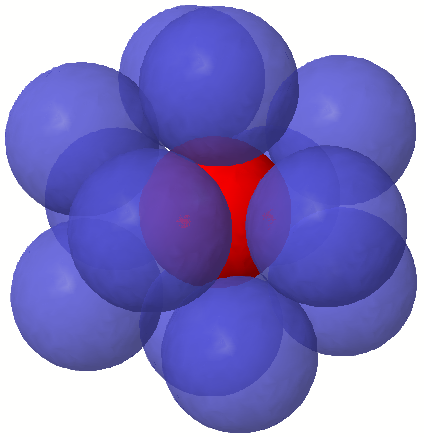
M12 has a nice construction based on the icosahedron. We place twelve ball-bearings around a central sphere (above), corresponding to the vertices of an icosahedron. An inverted twist is an operation where you choose a ball-bearing and its five neighbours, rotate them by 72°, and reflect the arrangement of ball-bearings in the centre of the central sphere. M12 is the group generated by an even number of inverted twists.

M24 can be constructed by a gadget known as the Miracle Octad Generator, which I’ll be explaining in more detail in about a fortnight. For M12, there is a smaller gadget known as the miniMOG (or ‘kitten’, alluding to the fact that ‘mog’ is an informal term for a cat!).

Icosians and the E8 lattice

So far, we have seen that there are real and complex constructions of the Leech lattice. There are also two quaternionic constructions, one of which is boring and analogous to the real and complex constructions. Instead, we’ll describe the more exciting construction, involving the (non-commutative) ring of icosians.

The icosians are a beautiful ring of quaternions with a large degree of symmetry. They are dense in the quaternions, and share some similarities with the integral elements of the quadratic field in the complex numbers. Whilst this quadratic field can be used to construct the Penrose tilings with fivefold symmetry, the icosians can be used to construct a four-dimensional quasicrystal with the H4 symmetry group possessed by the 120-cell.

The icosians are finite sums of unit icosians, of which there are 120. These include the 24 Hurwitz integers together with the 96 even permutations of ½(0, ±1, ±ψ, ±φ), where φ and ψ are the golden ratio and its Galois conjugate. The unit icosians under multiplication form the binary icosahedral group of order 120, which is the double cover of the icosahedral group.

It is trivial to observe that every icosian is of the form [(a + b√5) + (c + d√5)i + (e + f√5)j + (g + h√5)k], where the variables are rational numbers. This is an icosian if and only if the vector (a, b, c, d, e, f, g, h) lies in a particular scaled and rotated copy of the E8 lattice. We can think of this as a bijection θ from the icosians to the points of the E8 lattice.

Then the Leech lattice can be described as (θ(x), θ(y), θ(z)), where x + y + z = 0 (mod h) and x = y = z (mod h*), where h = ½(−√5 + i + j + k) and h* is its conjugate. We also have a dense three-dimensional quaternionic lattice, L, which is formed by the corresponding points (x, y, z).

Observe that the point symmetry group of the icosians is H4, of order 14400, whereas the point symmetry group of the E8 lattice is the Weyl group of E8, of order 696729600. Hence, there is no reason to assume that L has the same symmetry group as the Leech lattice (described later), and indeed it doesn’t. Whereas the symmetries of the Leech lattice form the double-cover of Conway’s sporadic group Co1, the symmetries of L form the double-cover of the Hall-Janko sporadic group J2. Similarly, the symmetries of the complex Leech lattice yield a setuple cover of the Suzuki sporadic group.

Theta series and automorphism group

To motivate the discussion of theta series, consider Problem 354 from the Project Euler website. This features a scaling of a hexagonal lattice, where the shortest vectors have squared norm 3 (so the Voronoi hexagons have a side length of 1). They provide a nice picture of this lattice:

The theta series is (the generating function of) the sequence giving the number of points at a specified squared distance. So, in this case, we obtain the theta series . The Project Euler problem asks how many of these coefficients below some large finite order are equal to 450.

The theta series of the square lattice gives the number of ways to express an integer as the sum of two squares of (not necessarily positive) integers. For the Leech lattice, the number of vectors of squared norm 2m is equal to , where τ is the Ramanujan tau function and σ₁₁ gives the sum of eleventh powers of divisors.

The first few terms of the theta series of the Leech lattice (A008408) are 1, 0, 196560, 16773120, 398034000, and so on. John Conway observed that the 398034000 vectors of squared norm 8 naturally partition into 8292375 ‘frames’ of 48 vectors positioned at the vertices of an orthoplex (generalised octahedron). Before we divide all vectors by √8 in the coordinate-based construction of the Leech lattice, one of these frames comprises all permutations of (±8,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0).

The automorphism group is transitive on these coordinate frames, and fixing a coordinate frame gives a subgroup 2^12.M24, corresponding to permutations and sign changes fixing the binary Golay code. By the Orbit-Stabiliser theorem, we recover the size of the automorphism group:

8292375 × 244823040 × 4096 = 8315553613086720000

This group is equal to its own automorphism group. It has a normal subgroup of index 2, which is Conway’s sporadic group Co1. The sporadic groups Co2 and Co3 are obtained by fixing additional points. We can also obtain many other sporadic groups in this manner, two of which are described in the next section.

Higman-Sims graph and McLaughlin graph

Take three lattice points that form the vertices of a triangle with side lengths of {2, √6, √6}. There are 100 lattice points of minimal distance 2 from all three of these three vertices. Consider these 100 points, and join two points with an edge if the distance is √6. The result is the Higman-Sims graph on 100 vertices. Claudio Rocchini produced the following drawing:

The Higman-Sims graph contains other exceptional graphs embedded within it. There are 352 ways that the vertices can be partitioned into two copies of the Hoffman-Singleton graph. Removing a vertex of the Higman-Sims graph together with its 22 neighbours gives the M22 graph.

We can also obtain the 275-vertex McLaughlin graph, by applying the same construction to a {2, 2, √6} triangle instead of a {2, √6, √6} triangle. The automorphism groups of the Higman-Sims graph and McLaughlin graph are the double covers of two more sporadic groups, the McLaughlin group and the Higman-Sims group.

If we take the convex hull of the 240 shortest vectors in the E8 lattice, we obtain the beautiful semiregular Gosset E8 polytope. The convex hull of the 196560 shortest vectors in the Leech lattice is a much more complicated object, but recently its structure was analysed. For each facet of the polytope, the authors construct a graph based on the lengths of its edges. The connected components of these graphs include:

• The Higman-Sims graph, Hoffman-Singleton graph, Johnson graph J(7,4), Tutte-Coxeter graph and Coxeter graph;
• Subdivisions of the Petersen graph, Franklin graph, triangular prism, and a bunch of small outerplanar graphs including trees.

Lorentzian lattices, string theory and the Monster Lie algebra

I was going to include this with the other constructions of the Leech lattice, but I’ve postponed discussion until now due to its depth, abstractness and amount of conjecture.

An elegant construction of the Leech lattice embeds it in (25+1)-dimensional Minkowski spacetime. In this spacetime, we use 25 spatial coordinates and one temporal coordinate, separated by a vertical line. We endow the space with an ‘inner product’ with signature (+, +, …, +|−).

The Lorentzian lattice II(25,1) consists of points such that:

• All coordinates are integers or all half-integers;
• The sum of coordinates is even.

The Leech lattice can be obtained from this by taking the lattice points r such that r.r = 2 and r.w = −1, where w = (0, 1, 2, 3, 4, …, 18, 19, 20, 21, 22, 23, 24, −70) is the Weyl vector, and ‘flattening’ it into Euclidean space whilst preserving the squared distances between points. Remarkably, w is a lightlike vector, since 0² + 1² + … + 24² = 70², as discovered by Edouard Lucas.

The Lorentzian lattice II(9, 1) is also of interest, being intimately related to the 9-dimensional hyperbolic tessellation which completes the sequence {triangular prism, truncated 5-simplex, E6 polytope, E7 polytope, E8 polytope, E8 lattice, …} of exceptional semiregular polytopes. However, II(9, 1) and II(17, 1) are not as exceptional as II(25, 1), since their Weyl vectors are not lightlike and the corresponding constructions give finite Coxeter-Dynkin diagrams instead of a copy of the Leech lattice.

Conway et al defined an infinite-dimensional Lie algebra based on the Leech roots (those vectors r such that r.r = 2 and r.w = −1), conjecturing that the Monster group occurs naturally as a subquotient of the automorphism group of a sub-algebra. An explicit Monster Lie algebra could be created by applying a particular string-theoretic theorem to a vertex algebra defined by Richard Borcherds.

People such as Stephen Wolfram, Konrad Zuse and Ed Fredkin proposed that our universe is a cellular automaton. One of the major criticisms is that, whilst cellular automata on hexagonal grids can exhibit large-scale SO(2) symmetry (lattice gases are examples), they lack Lorentz invariance. This problem could possibly be circumvented by cellular automata on Lorentzian lattices such as II(9,1) or II(25,1), which exhibit a discrete group of symmetries including Lorentz transformations. Indeed, a particularly well-chosen cellular automaton on II(9,1) or II(25,1) would be a discretised version of 10- or 26-dimensional string theory.

(This article apparently has precisely 3000 words, making it the longest cp4space post so far…)

The Perrin sequence is defined by a recurrence relation, and is qualitatively similar to the Lucas sequence. The initial terms are and subsequent terms are defined by , and summarised in the following spiral of equilateral triangles:

As you can see, I’ve cheated slightly by tucking a corner of beneath . This is because the spiral was designed for the Padovan sequence, which is to the Perrin sequence as the Fibonacci sequence is to the Lucas sequence. This analogy can be made precise by considering the closed form of the Perrin sequence:

These Greek letters are the roots of the characteristic polynomial x³ − x − 1 = 0. They can be computed by an easy application of Tartaglia’s method for solving the cubic, but the resulting expression is messy and not particularly insightful. The closed form, however, can be used to deduce that if p is prime, then p divides P(p):

modulo p.

The non-trivial step can be deduced by expanding the expression , which gives p multiplied by some symmetric polynomial (as all non-trivial multinomial coefficients are divisible by p), which in turn can be expressed as a polynomial in the elementary symmetric polynomials (thanks to Newton’s theorem), which are all integers (by Vieta’s formulae). This result is a massive generalisation of the freshman’s dream.

A nicer way to prove that p divides P(p) is by noticing that P(p) counts the number of ways to tile an order-p cycle graph with tiles of length 2 or 3 (or, equivalently, the number of maximal independent sets). Here is an example tiling for p = 17:

When acted upon by the cyclic group Cp of rotations, no tiling can have a non-trivial stabiliser. Hence, the tilings are partitioned into orbits of size p, so the total number of tilings must be divisible by p. This argument generalises to any depressed monic polynomial with integer coefficients, as does the proof involving multinomial coefficients.

This can be exploited to give a Fermat-style test for primality. If n does not divide P(n), then n must be composite. We can compute this residue in O(log² n log log n log log log n) by using a matrix form of the recurrence relation, repeated squaring and the Schönhage-Strassen algorithm for multiplication.

Perrin pseudoprimes appear to be rarer than Fermat pseudoprimes, with only 17 below 10^9 compared with 646 Carmichael numbers and 5597 base-2 pseudoprimes in this interval. The smallest is 521² = 271441, followed by 904631 and 16532714. It’s possible to make better primality tests by (for instance) combining the Perrin, Lucas and Fermat primality tests. I don’t know of any composite numbers that are simultaneously Perrin and Lucas pseudoprimes, but they most probably exist.

Occasionally, some of my ciphers have the frustrating property that whilst easy to realise what to do, they can still be incredibly long-winded to solve. I can imagine that this is one such cipher:

I apologise for the profusion of Petersen graphs.

In the not-too-distant future, people are going to be celebrating the 100th birthday of Bill Tutte. He’s not quite as well-known as Alan Turing, which is a shame since they were both equally invaluable in the cryptanalysis at Bletchley Park. You may also know him from the problem of squaring the square, which he accomplished with three of his friends whilst they were students at Trinity. The story of how they met was rather interesting and extremely serendipitous, and is recounted at the beginning of this article on squaring.net.

The catalysis for this was a complete chance encounter in London between Trinity mathmos Arthur Stone and Cedric Smith, who happened to both reside in the area. The scope of the conversation was as vacuous as the empty set, and not even their names were exchanged at the time. Much more interesting was the next edge of the acquaintance graph, which was created in an equally improbable manner:

As first-year undergraduates, Cedric Smith met Rowland Brooks in a lecture on almost periodic functions. This was the equivalent of a Part III lecture, and their attendance was the result of an error in a timetable. This administrative mistake became apparent from the incomprehensibility of the lecture! Nevertheless, it was very fortunate that the timetables were erroneous, since it ultimately led to a very productive union of four mathematicians.

The fourth, of course, was Bill Tutte, who was reading chemistry (which has since been engulfed into the Natural Sciences Tripos) as well as mathematics. He knew Rowland Brooks, and later met Smith and Stone by extension. Tutte will be the primary focus of the majority of this article, so it seems appropriate to include a picture. Even better, here is a photograph of a bronze bust by the accomplished sculptor, artist, painter and former musician, singer and actress, Gabriella Bollobás, who happens to be married to the eminent mathematician Professor Bollobás:

Sculpture of Bill Tutte by Gabriella Bollobás

Squaring the square

The four of them met on a regular basis to discuss mathematical problems. One of these was the problem of finding a squared square, that is to say a dissection of a square into a finite number of smaller squares, no two of which are the same size. William Tutte wrote a detailed account of their effort to solve this mathematical problem, which spanned the years 1936 through to 1938.

The first major insight was that a squared rectangle could be represented by a network of one-ohm resistors, where the Thevenin equivalent resistance is equal to the aspect ratio of the squared rectangle. Specifically, imagine that the rectangle is made from a material of uniform resistivity, where a square of the material has a resistance of one ohm between opposite edges. Then, given a dissection of the rectangle into squares, we can replace each horizontal line with a perfect conductor, and each vertical line with a perfect insulator, and since all current flows vertically this has no effect on the total resistance.

A corollary of this is that the resulting squared rectangle must have sides in a ratio corresponding to the resistance of a circuit composed of one-ohm resistors; this forces it to be rational. Tutte et al also showed that the dimensions of the constituent squares must also be commensurate with the side lengths of the rectangle.

The next important discovery was by Smith’s mother, who assembled the squares into a perfect rectangle in a different arrangement from the original configuration. Eventually, it was noticed that this corresponded to a resistance-preserving transformation of the corresponding electrical circuit. They reasoned that it might be possible to tile the same rectangle with two completely different sets of squares, which would trivially result in a squared square:

Problematically, the squared rectangle produced by Smith’s mother featured precisely the same set of squares as the original, so the resulting dissection of the square would be replete with pairs of identical squares. Hence, further ingenuity was required to discover a perfect squared square.

The structure of Smith’s circuit was observed to naturally partition into a ‘rotor’ with threefold rotational symmetry and a ‘stator’. With a one-wire stator, it was realised that it could be possible to produce two rectangles sharing only one common square, which could be overlapped to yield a configuration trivially completable into a squared square. It transpires that Smith and Stone collaboratively found one, at almost precisely the same time that Brooks did so.

These order-69 squares were the first to be discovered, but far from being optimal. The Trinity Mathematical Society logo is an order-21 squared square, which has been proved to be minimal by exhaustive search.

Cryptanalysis of the Lorenz cipher

A year later, Britain and Germany plunged into the Second World War. (I’m not going to mention the war again, I promise!) This involved quite a lot of secret communication on both sides, and much of the Allied codebreaking efforts were concentrated in Bletchley Park.

Bletchley Park defeated two great ciphers. The first of these, which is probably more well known, was Arthur Scherbius’ Enigma cipher used by the Luftwaffe and Kriegsmarine. The effort began with the Polish mathematician Marian Rejewski. He knew roughly how the Enigma worked from models stolen by intelligence agencies, but had to embrace the immense challenge of determining both the internal wiring of the rotors and a method for cryptanalysing the variable key (which changes with each day). Rejewski built a machine, the bomba, for brute-forcing the key settings. Eventually, the Polish intelligence passed their discoveries to Bletchley Park, where people such as Alan Turing (King’s College, Cambridge) and Gordon Welchman (Trinity, yet again) found alternative and more flexible methods of cryptanalysing the Enigma based on Rejewski’s insights.

However, the cryptanalysis of the more difficult Lorenz cipher was an infinitely more impressive achievement, mainly because it was accomplished without anyone having ever seen one of the Lorenz encryption machines. I shall briefly describe its modus operandi.

The Lorenz cipher used the Baudot code, where each character is represented by five binary digits (either dots or crosses). The enciphering machine (or Schlüsselzusatz) produced a pseudorandom stream of information which was XOR’d with the plaintext to yield a ciphertext. The same stream of information, when XOR’d with the incoming ciphertext, would result in perfectly comprehensible plaintext. This Vernam cipher was a known form of encryption, but cryptanalysists at Bletchley Park had no idea how the pseudorandom bit generator operated.

What would be helpful is if the output of the pseudorandom bit generator could actually be isolated. This happened when a lazy operator was asked to repeat a message with the same key, and abbreviated it slightly, giving a huge vulnerability. Specifically, XORing the two encrypted messages would neutralise the contribution of the Schlüsselzusatz, giving the symmetric difference of the two messages. John Tiltman was able to carefully separate this into the two original messages, treating it as a basic autokey cipher. Moreover, he could XOR the encrypted and decrypted messages to isolate the output of the Schlüsselzusatz.

Enter Tutte. Tutte was given the output of the Schlüsselzusatz, and asked to deduce the internal workings of the machine. This, of course, was an incredibly difficult task. He started by looking for approximate periodicity (perhaps the lecture on almost periodic functions helped!) in the bitstream. He found a period-41 pattern, suggesting the presence of a rotor χ1 with 41 teeth. Moreover, he determined that another more complicated rotor (ψ1) driven by a motor wheel μ contributed to the encryption. Proceeding in this manner, cryptanalysts determined how each of the other four bits were generated (there were five independent mechanisms with coprime periods).

Armed with Tutte’s deduction, Alan Turing et al were able to work on algorithmically cracking this cipher. This began with the electromechanical Heath Robinson machines, which were replaced by the much more efficient electronic Colossus computers, designed and built by engineer Tommy Flowers. Gordon Welchman was somewhat disapproving of this shift from good old electromechanical relays to those new-fangled thermionic valves; fortunately, Turing was more forgiving. Nowadays, of course, relays and valves have both been rendered obsolete by microscopic transistors on silicon chips, and may eventually be further antiquated by advances in carbon nanotechnology.

The intercepted and decrypted communications gave the Allies a massive advantage. I seem to recall that they even sent a Lorenz-encrypted message to sabotage the Nazi military by issuing unhelpful orders, although I might be confusing this with the Sherlock Holmes mystery, The Adventure of the Dancing Men.

Graph theory

Squaring the square, whilst initially appearing to be combinatorial geometry, eventually succumbed to a graph-theoretic approach. Many of Bill Tutte’s mathematical accomplishments were in graph theory, including the disproof of Tait’s conjecture that every 3-regular polyhedral graph admits a Hamiltonian cycle.

He has a few graphs named after him, one of which is the Tutte 8-cage. This is a 3-regular graph with girth 8, and indeed is the unique smallest such graph. It possesses a large amount of symmetry, a small amount of which is apparent in the following picture:

Its full symmetry group is PΛL(2,9), the automorphism group of S6. This is apparent from the standard construction of the 8-cage: take the 15 unordered pairs of letters {a,b,c,d,e,f}, together with the 15 unordered triples of unordered pairs (such as (ac,bf,de)), and connect a triple to a pair when they are incident. This has an obvious action of S6 (permuting the letters), but also features an outer automorphism interchanging the two halves of this bipartite graph. Indeed, this is one of the simplest ways to see the outer automorphism of S6.

Tutte was also responsible for the snark conjecture, that every snark contains the Petersen graph as a minor. When proved much later by Robertson, Seymour et al, this gave an indirect proof of the four colour theorem as an immediate corollary. Other theorems include the BEST theorem (where the ‘T’ in the acronym stands for ‘Tutte’), Tutte-Berge formula and Tutte’s homotopy theorem.

William Tutte passed away in 2002, after a long life (by contrast with Turing’s untimely cyanide-laced Rosacaean death) and a very fruitful and productive mathematical career. There is an obituary in the Guardian.

Suppose you were cast away on a desert island. You’re only allowed to take a maximum of eight known theorems with you, along with rudimentary results such as ZFC axioms together with ’boring stuff’ such as mathematical induction over the naturals, commutativity of real multiplication and the least upper-bound property of . Everything else you have to prove yourself.

So, which eight theorems would you take with you on a desert island? It would be a waste of time to take the Baire category theorem, for instance; despite being extremely useful, it’s pretty trivial to prove. The same applies to the Dirichlet pigeonhole principle. On the other end of the spectrum, whilst Fermat’s Last Theorem is very difficult to prove, the end result is not nearly as useful as the machinery developed by Andrew Wiles in the course of solving this problem.

At the end of the post, there’s a ‘comments’ section for you to mention which theorems you would choose if marooned on a desert island. Here are my choices:

8. Density Hales-Jewett theorem

The ordinary Hales-Jewett theorem is quite straightforward to prove, using plenty of induction and the Dirichlet pigeonhole principle. On the other hand, the density analogue (c.f. Szemeredi’s theorem) is much deeper, requiring the entire Polymath project to establish a purely combinatorial proof (the original proof involved ergodic theory).

I’m not sure whether I’ve ever required the full force of Density Hales-Jewett, but Szemeredi’s theorem and ordinary Hales-Jewett have proved invaluable to me.

7. The abc theorem

Disclaimer: I don’t think that a second person is capable of understanding Mochizuki theory*, so this might still be classed as a conjecture until someone can peer-review the paper.

* Formerly known as inter-universal Teichmüller theory, although Doron Zeilberger makes a good argument that it should be renamed.

The abc conjecture is concerned with triples of coprime naturals, a < b < c, such that a + b = c. It states that the radical d (larger squarefree divisor) of abc cannot be much smaller than c. Specifically, for any ε > 0, we can only find finitely many examples where . This asserts that Beal’s conjecture holds in all but a finite number of cases, as does Fermat’s last theorem.

6. Max-flow min-cut theorem

I would have ranked this higher, except for the fact that it has a short elementary proof. The statement of the theorem is about networks, which are directed (multi-)graphs where each edge has a maximum capacity. A flow in a network is an assignment of nonnegative real values to each of the edges, such that they do not exceed the capacity, and that Kirchoff’s current law is obeyed at all vertices (with the exception of the source and sink vertices). The statement of the theorem is that the maximum flow attainable is equal to the minimum capacity of a cut (partitioning of the graph into two sets of vertices, so as to separate the source from the sink).

It can be used to prove Menger’s theorem in graph theory, Hall’s marriage theorem, Dilworth’s theorem on partially-ordered sets, and the Erdős-Szekeres theorem (although this also follows from Dilworth’s easier twin, Mirsky’s theorem).

5. Borsuk-Ulam theorem

This is informally stated as ‘two antipodal points on the Earth’s surface have the same temperature and pressure’. More generally, if we have a continuous function f from the n-sphere to , then we can find antipodal points x and y such that f(x) = f(y).

A corollary is the Brouwer fixed-point theorem, and all that that implies.

4. Gödel’s completeness theorem

This is one of the most beautiful and powerful theorems in mathematical logic. If a statement in first-order logic is consistent (i.e. we cannot prove a contradiction), then this asserts that there exists a finite or countable model. Consequently, we establish logical compactness: a set of first-order sentences has a model if and only if every finite subset has a model.

With the compactness theorem, the problem of computing the chromatic number of the plane is reduced to the more tractable problem of determining the maximum chromatic number of any finite unit-distance graph.

3. Every set can be well-ordered

This is equivalent to the axiom of choice, but much friendlier than the boring statement of AC involving a choice function. The main advantage is that it endows one with the power of transfinite induction over arbitrary sets, which is one of my favourite tools for proving theorems:

• Constructing an infinite game where neither player has a winning strategy;
• 2-colouring the plane such that there is no continuous monochromatic path;
• Proving that the direct product of two infinite sets has cardinality equal to the larger of the two sets (by Cantor normal form);
• Establishing Zorn’s lemma to show that any vector space has a basis…

2. Classification of finite simple groups

This is an impossible endeavour for a single individual to attempt, with the current proof being a 5000-page behemoth comprising many different papers. The Classification obviously reduces deep results such as the Feit-Thompson theorem (that there are no finite simple groups with odd composite order) and Burnside’s theorem to easy corollaries. (Of course, these theorems were almost certainly used in establishing the Classification, so this would be logically circular.)

It’s also a very beautiful theorem, with a vast wealth of exciting groups such as PSL(2,7), exceptional Lie groups over finite fields, and the Monster group. The Classification was also involved in proving theorems in areas outside group theory, such as establishing which graphs are 4- and 5-ultrahomogeneous.

1. Bezout’s theorem

This is a result in geometry, which says that if a degree-m and degree-n algebraic curve intersect in finitely many points, then they do so in at most mn points. Moreover, equality holds when the curves are on the complex projective plane, and we count intersections with the appropriate multiplicity.

An immediate corollary of this is the fundamental theorem of calculus, by taking one of the curves to be the line y = 0 and the other to be y = f(x) (where terms have been multiplied by appropriate powers of z to homogeneise them, and f is an arbitrary polynomial).

Also, it can be used to establish the Cayley-Bacharach theorem of cubic curves, which itself can prove the associativity of the elliptic curve group operation, Pascal’s theorem, Pappus’ theorem, and thus Desargues’ theorem.

Here are some primarily mathematical double-entendres conceived by members of the Trinity Mathematicians’ Alcoholic Society. Some of them are biological or particle-physical, but never mind. Also, some names are censored for legal reasons.

Disclaimer: I accept no responsibility for any offence caused by these; if you’re offended, comment and I shall endeavour to respond to the best of my ability.

• I’m like the Riemann zeta function; I have a massive pole — Emperor of TMAS (me)
• You put a whole new angle on — Empress of TMAS
• I’m so smooth, I’m infinitely differentiable — Vice-President of TMAS
• I’m like the blancmange function; I’m tasty and not well-behaved — Emperor of TMAS (me)
• You’re a photon, because you make my light shine — First Gentleman of TMAS
• If I were an enzyme, I’d be helicase so I could unzip your genes — Humphrey Galbraith, nephew of Lord Strathclyde
• You’re the integral of — Joe Tomkinson
• I wish you were my maths example sheet, because then I’d turn up to my supervision and explain why I didn’t do you properly — Vice-President of TMAS
• If I were endoplasmic reticulum, would you like me rough or smooth? — Sara Devereux
• I wish you were my maths example sheet, because I’d do you even if I didn’t understand you. — First Gentleman of TMAS
• I wish you were an integral, because then I could substitute and do you anyway — Humphrey
• My girlfriend is like the integral of ; I can’t do her without cheating — Vice-President of TMAS
• I wish you were my multiplicative inverse, because together we’d be one — First Gentleman of TMAS
• I wish I were your derivative, because then I could lie tangent to your curves — a fellow RMM gold medallist
• If I were a Schwarz cell, I’d be on your axon for some fast-action potential — Anonymous
• My love for you is unbounded and monotone increasing — Empress of TMAS
• She’s like an asymptote; I get closer and closer but never reach her — Communal effort
• If I were , you would be ; I’d be contained in you — Ryan Wilson
• Our intersection is very pleasurable, let’s try our union…? — Joe Tomkinson
• Particle physics really gives me a hadron — First Gentleman of TMAS
• If you were , I’d be , because then we’d be osculating — the same fellow RMM gold medallist
• Our love is like the naturals and the ocean floor; it’s deep and infinite — First Gentleman of TMAS
• I’m like a rigorously proved theorem; I can last forever — Emperor of TMAS (me)
• Are you an electron, because then you’d be lepton? — Anonymous
• You are my only element; without you I’d be empty — First Gentleman of TMAS
• You’re like a sporadic group, beautiful and mysterious — Emperor of TMAS (me)

Breaking news: A £500 prize for the most elegant solution in the British Mathematical Olympiad has been founded in the memory of Christopher Bradley, whose contributions to the United Kingdom Mathematics Trust were both plentiful and invaluable. Amongst his portfolio is the bestselling Plane Euclidean Geometry (coauthored with Anthony Gardiner), which explores the interactions of algebraic curves of low degree in two dimensions from a synthetic perspective.

The advantage of this new prize is that it discourages ridiculously long case-bashes, thus making the BMO easier for us to mark. Some case-bashes are long but morally simple, such as the proof of the four-colour theorem, and it is difficult to assess whether such proofs are elegant. Nevertheless, in most cases it is easy to distinguish between an elegant solution and an inelegant one. For instance, consider the following problem:

What is the maximum number of subsets of {1, 2, 3, …, n} such that no subset is a subset of a different subset?

If we choose subsets of the same cardinality, then it’s obvious that these would satisfy the criterion. For example, with {1, 2, 3, 4} and choosing the size-2 subsets, we obtain the following six sets:

• {1, 2}
• {3, 4}
• {1, 3}
• {2, 4}
• {1, 4}
• {2, 3}

This strategy is maximised when the cardinalities of the subsets are as close to ½n as possible. It is difficult to imagine a more optimal solution, and it is a theorem (Sperner’s theorem) that this is actually the best we can manage.

Anyway, a trivial rephrasing of the problem is:

What is the maximum length of an antichain in the lattice of subsets of {1, 2, …, n}, ordered by inclusion?

By Dilworth’s theorem (a corollary of max-flow min-cut), this is equivalent to:

What is the minimum number of chains into which we can partition the lattice of subsets of {1, 2, …, n} ordered by inclusion?

We can think of the subsets of {1, 2, …, n} as being vertices of a hypercube. All of the automorphisms of the hypercube fixing the vertex corresponding to the empty set are symmetries of Sperner’s theorem.

It would be nice to have a generalisation of this theorem which has all automorphisms of the hypercube as symmetries (i.e. the empty set is not given privileged status). Such a generalisation was very recently discovered by Hunter Spink in the process of proving an open problem about the maximum number of strict maxima of quadratic functions of n Boolean variables. The short but exciting paper can be found here.

So, yes, Hunter Spink is rather awesome. We were discussing the completely unrelated topic of the existence of a ‘romantic’ clearing between a Salix and a Sorbus just south of the bridge of King’s College, Cambridge. It is only just possible to punt into the clearing, perform a U-turn, and exit.

The clearing at 52.203650° N, 0.113854° E.

As I was describing this, Richard Freeland mentioned the well-known problem of finding the clearing with minimum area corresponding to the constraint that one can rotate a punt (considered to be a line segment) 360° within it. A reasonably good solution is the deltoid:

Surprisingly, it transpires that there is no minimum area attainable. For every positive ε, we can find a simply-connected set of area < ε in which a punt can be rotated. However, the infimum of 0 cannot be obtained, i.e. there is no set of zero Lebesgue measure in which we can rotate a punt (c.f. this proof by Terence Tao). There are, however, measure-zero fractal sets obeying the strictly weaker property of containing a unit line segment in every orientation, so-called Besicovitch sets.

Generalisations to have been considered, but this problem was found to be very difficult. As a compromise, people contemplated the analogy over finite fields: fix n > 2 and let p vary. Then, we can find a non-zero lower bound for the density of a Besicovitch set (containing a line in every direction) in the vector space , depending only on n and not p.

Dvir found a beautiful proof (which would certainly win Bradley’s elegance prize!), again mentioned in an article by Terry Tao.

This one is entirely graphical:

Thanks go to James Aaronson for the design.

It is a well-known fact, attributed to Cantor, that the set of rationals is countably infinite or, equivalently, we can find a bijection between the rationals and integers. These are easy to construct, but typically quite ugly. If you want a closed-form bijection, you have to work harder, but it’s still possible.

My favourite enumeration of the (non-negative) rationals was discovered by Moshe Newman, and is a simple recurrence relation. More specifically, it is a very basic function f such that the sequence {0, f(0), f(f(0)), f(f(f(0))), …} contains each non-negative rational precisely once.

If you’re not amazed by this, you should be. It generates the sequence {0/1, 1/1, 1/2, 2/1, 1/3, 3/2, 2/3, 3/1, 1/4, 4/3, 3/5, 5/2, 2/5, 5/3, …}, which can be proved to hit every non-negative rational exactly once (indeed, if it repeated a rational, it would become cyclic). Also, note that the denominator of one term is equal to the numerator of its successor, yielding the following sequence of positive integers:

0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, … (sequence A002847 in OEIS)

This sequence, Stern’s diatomic sequence, is highly intriguing. We define the nth term to be fusc(n), so fusc(0) = 0 and fusc(1) = fusc(2) = 1, for example. There are several equivalent ways to define the fusc function:

• The rational counter description gives the second-order recurrence relation fusc(n) = fusc(n−1) − fusc(n−2) + 2 fusc(n−1) floor(fusc(n−2)/fusc(n−1)).
• There’s also the David-Monk-style pair of recurrence relations, fusc(2n) = fusc(n) and fusc(2n+1) = fusc(n) + fusc(n+1).
• The previous definition can be seen to be equivalent to the definition of fusc(n) as the number of ways of writing n as a sum of powers of two, such that no power of two appears more than twice.
• fusc(n) is also the number of odd binomial coefficients of the form .

But yes, this is all pretty impressive. The sequence given by Newnham’s rational counter is a breadth-first traversal of the Calkin-Wilf tree, as shown below in this picture by David Eppstein:

Each node has children and . It is a routine exercise (which, I believe, has appeared on the British Mathematical Olympiad) to show that each positive rational appears precisely once in this binary tree.

The 50-pence and 20-pence coins are regular curvilinear heptagons, where each edge is a circular arc centred on the opposite vertex.

One may ask why the coins have such an unusual shape. One possible answer is that it is impossible for a counterfeiter to forge with just a compass, straightedge and sheet of cupronickel. However, since compass-and-straightedge constructions are seldom used in practice, this is clearly not the reason.

This curvilinear heptagon has another property, which is easiest to demonstrate with its triangular analogue, the Reuleaux triangle. It is a curve of constant width, which means that all of its axonometric shadows are line segments of equal width. Equivalently, when rolled on a flat surface, the height of the coin remains constant.

The reason for employing a curve of constant width is that it can be more easily recognised by mechanical coin-detecting machines. The Reuleaux polygons are not the only curves of constant width, however, since we can easily design irregular curvilinear polygons with this property. Again, these are all piecewise circular.

The next question is whether there exist curves of constant width which are not piecewise circular. Intuitively, the answer is yes, since it seems plausible that a limiting process could be applied where the lengths of the circular arcs tend to zero. A more rigorous formulation is given by the following system of differential equations, where (as functions of t) are the endpoints of the line:

• a × k = b × k = 0 (both endpoints lie in the ij-plane);
• a’ · (a − b) = b’ · (b − a) = 0 (the endpoints move perpendicularly to the line segment, preserving its length);
• a’ × (a − b) · k ≥ 0 and b’ × (b − a) · k ≥ 0 (the endpoints move in the same direction);
• a(t + T) = b(t) and b(t + T) = a(t) (the curve is closed).

It transpires that there are algebraic curves other than the circle, which have constant width. One example is a degree-8 curve discovered by Stanley Rabinowitz.

Solids of constant width

The obvious generalisation of the Reuleaux triangle to three dimensions, the Reuleaux tetrahedron, does not have constant width. Nevertheless, Meissner demonstrated that it is possible to modify three of the edges of the tetrahedron to yield an actual surface of constant width, the Meissner tetrahedron.

Meissner tetrahedra can be obtained commercially from Maths Gear.

You may have wondered why the last few ciphers have been erratic. The answer is so that the 50th cipher will land exactly on Professor Imre Leader‘s 50th birthday, which was celebrated 14 hours ago. One of the main components of the celebration was this Othello cake I assembled from an existing cake, a layer of fruit compote, a sheet of icing, chocolate buttons of two varieties, and candles:

Mapping a square Othello board on a circular cake is easy, thanks to the famous Riemann mapping theorem. If Imre played three-dimensional Othello, then that would no longer be the case, as Liouville’s theorem asserts that the only conformal maps in three or more dimensions are Möbius transformations.

The birthday card was signed by fourteen A4 sheets of people, and featured the following pursuit-and-evasion problem inspired by an analogue on the edges of a tetrahedron. A name has been censored for legal reasons:

I believe that Gabriel Gendler was the first to solve this version of the problem. We also made a related board game by discretising space and time:

Anyway, here is the cipher, which you should decipher and follow as soon as possible:

Jnvg ba cbaf qryrpgngvbavf hagvy zvqavtug. Ybbx ng (2π/3, π/6).
Gur cnffjbeq vf va ybjre-pnfr.

Good luck.